Getting the Skeleton Files
As usual, run git pull skeleton master to get the skeleton files.
Introduction
In this assignment, we'll be building an artificial intelligence that solves puzzles. Specifically, given an object of type WorldState, your solver will take that WorldState and find a sequence of valid transitions between world states such that the puzzle is solved.
As an example of one such puzzle, consider trying to convert one word in English to another by either changing, adding, or removing letters such that every transition results in a valid English word. Suppose we start with the word "horse" and we want to turn it into "nurse". To do this, we could perform the following transitions: horse -> hose -> hole -> cole -> core -> cure -> pure -> purse -> nurse.
As another example, consider the 8-puzzle problem. The 8-puzzle is a puzzle invented and popularized by Noyes Palmer Chapman in the 1870s. It is played on a 3-by-3 grid with 8 square tiles labeled 1 through 8 and a blank square. In this puzzle, the goal is to rearrange the tiles so that they are in order, using as few moves as possible. The player is permitted to slide tiles horizontally or vertically into the blank square. The following shows a sequence of legal moves from an initial board (left) to the goal board (right). Each of these puzzles is considered a valid "WorldState".
1 3 1 3 1 2 3 1 2 3 1 2 3
4 2 5 => 4 2 5 => 4 5 => 4 5 => 4 5 6
7 8 6 7 8 6 7 8 6 7 8 6 7 8
initial 1 left 2 up 5 left goalIn this assignment, not only must your artificial intelligence find a solution to any WorldState puzzle, but it must also be the shortest possible solution. While this may seem daunting, read on, and you'll see that it's not so bad.
Puzzle Formalization
In this assignment, all puzzles will be implementations of the WorldState interface, given below.
package hw3.puzzle;
public interface WorldState {
/** Provides an estimate of the number of moves to reach the goal.
* Must be less than or equal to the correct distance. */
int estimatedDistanceToGoal();
/** Provides an iterable of all the neighbors of this WorldState. */
Iterable<WorldState> neighbors();
default public boolean isGoal() {
return estimatedDistanceToGoal() == 0;
}
}That is, the WorldState implementation must have a method to return all neighbors, as well as the distance to the goal. For example, suppose our WorldState is the word horse with goal nurse. In that case, neighbors would return ["house", "worse", "hose", "horses"], and estimatedDistanceToGoal might return 2, since changing h into n and o into u would result in reaching the goal. Note that the exact behavior for estimatedDistanceToGoal is not well defined. So long as the estimate is less than or equal to the actual distance to the goal, the estimate is considered valid. In this example, the actual distance is 8 (see example above) and thus the estimate is valid.
Best-First Search
Your AI will implement the A* search algorithm.
Before we describe this algorithm, we'll first define a search node of the puzzle to be:
- a
WorldState. - the number of moves made to reach this world state from the initial state.
- a reference to the previous search node.
The first step of the algorithm is to create a priority queue of search nodes, and insert an "initial search node" into the priority queue, which consists of:
- the initial world state.
- 0 (since no moves have been made yet).
- null (since there is no previous search node).
The algorithm then proceeds as follows:
- Remove the search node with minimum priority. Let's call this node X. If it is the goal node, then we're done.
- Otherwise, for each neighbor of X's world state, create a new search node that obeys the description above and insert it into the priority queue.
We can think of each search node as having a priority equal to the sum of (the number of moves made to reach this world state from the initial state + the WorldState's estimatedDistanceToGoal). In other words, if we have two search nodes on the priority queue, with the first M1 moves away from the initial state and E1 as its estimated distance to goal, and the other having M2 moves so far and E2 as its estimated distance to goal, then the former search node will have a lower priority iff (M1 + E1) < (E2 + M2).
The A* algorithm can also be thought of as "Given a state, pick a neighbor state such that (distance so far + estimated distance to goal) is minimized. Repeat until the goal is seen".
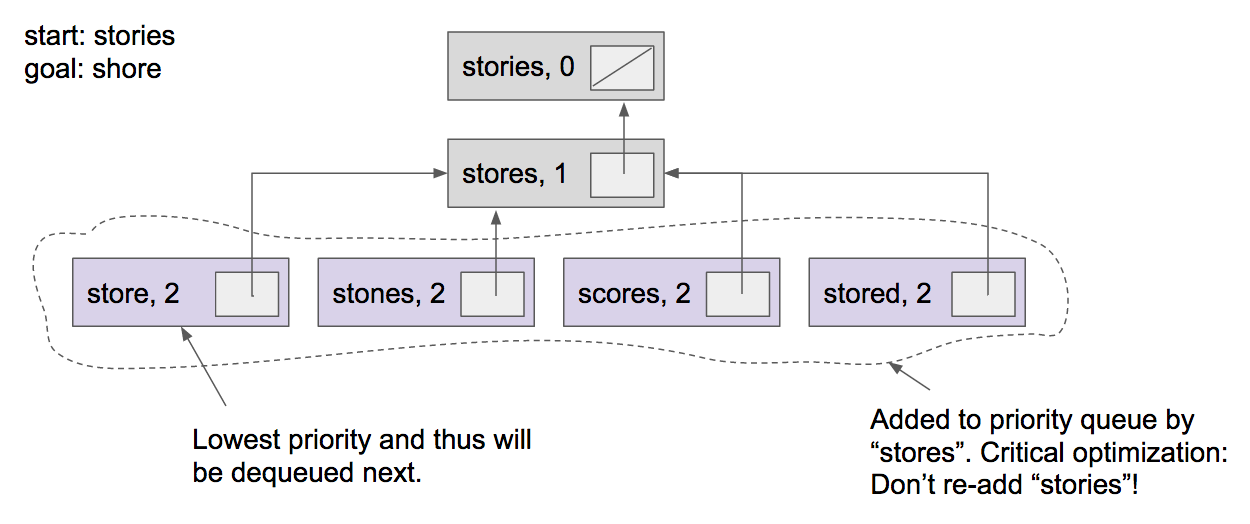
As an example, consider the problem of converting the word "stories" into "shore". The diagram below shows the six search-nodes created after two removals, i.e. after "stories" has had a chance to be X, and "stores" has had a chance to be X. At this point in time, the priority queue contains four search nodes, and the next node to be dequeued will be "store", for which M = 2 and E = 1. The critical optimization mentioned in the figure is described below under "Optimizations".
To see an example of this algorithm in action, see this video or these slides.
Solver
Create an immutable Solver class with the following API:
public class Solver {
public Solver(WorldState initial)
public int moves()
public Iterable<WorldState> solution()
}Where the methods work as follows:
Solver(initial): Constructor which solves the puzzle, computing
everything necessary for moves() and solution() to
not have to solve the problem again. Solves the
puzzle using the A* algorithm. Assumes a solution exists.
moves(): Returns the minimum number of moves to solve the puzzle starting
at the initial WorldState.
solution(): Returns a sequence of WorldStates from the initial WorldState
to the solution.To implement the A* algorithm, you must use the MinPQ class from edu.princeton.cs.algs4 for the priority queue.
Test out your code using the WordPuzzleSolver class. If implemented properly, you should get a path between "cube" and "tubes". Try changing the start state to "horse" and the end state to "nurse", and you should get the solution horse -> hose -> hole -> cole -> core -> cure -> pure -> purse -> nurse. Other solutions of the same length are technically correct, but for full credit on this assignment, you'll need to implement the critical optimization described below. If you get "horse -> hose -> home -> come -> core -> cure -> pure -> purse -> nurse", most likely you have not implemented the critical optimization properly.
Hint: Recall the search node concept mentioned above for using your PQ.
Optimizations
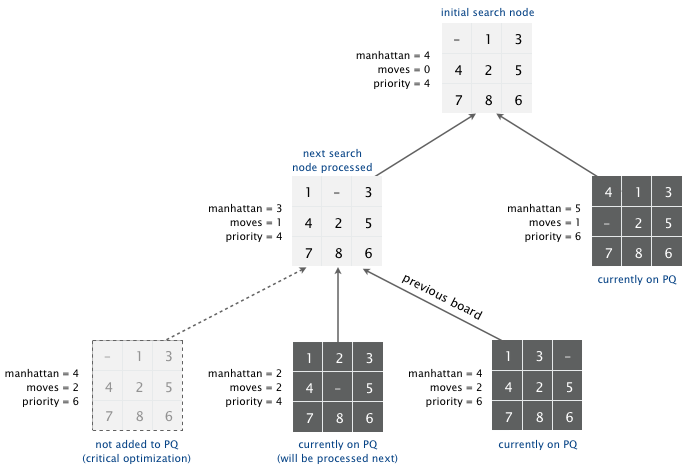
A critical optimization: Best-first search has one annoying feature: search nodes corresponding to the same board are enqueued on the priority queue many times. To reduce unnecessary exploration of useless search nodes, when considering the neighbors of a search node, don't enqueue a neighbor if its world state is the same as the world state of the previous search node. You must implement this optimization, otherwise your code will not be fast enough for the second part of this assignment or the Gradescope autograder.
A second optimization: To avoid recomputing the estimatedDistanceToGoal() result from scratch each time during various priority queue operations, compute it at most once per object; save its value in an instance variable; and return the saved value as needed. This caching technique is broadly applicable: consider using it in any situation where you are recomputing the same quantity many times and for which computing that quantity is a bottleneck operation.
Board
For the second part of this assignment, you'll implement the Board class, allowing your Solver from part 1 to solve the 8-puzzle.
Organize your program by creating an immutable Board class with the following API:
public class Board implements WorldState {
public Board(int[][] tiles)
public int tileAt(int i, int j)
public int size()
public Iterable<WorldState> neighbors()
public int hamming()
public int manhattan()
public int estimatedDistanceToGoal()
public boolean isGoal()
public boolean equals(Object y)
public String toString()
}Where the constructor and methods work as follows:
Board(tiles): Constructs a board from an N-by-N array of tiles where
tiles[i][j] = tile at row i, column j
tileAt(i, j): Returns value of tile at row i, column j (or 0 if blank)
size(): Returns the board size N
neighbors(): Returns the neighbors of the current board
hamming(): Hamming estimate described below
manhattan(): Manhattan estimate described below
estimatedDistanceToGoal(): Estimated distance to goal. This method should
simply return the results of manhattan() when submitted to
Gradescope.
isGoal(): Returns true if is this board the goal board
equals(y): Returns true if this board's tile values are the same
position as y's
toString(): Returns the string representation of the board. This
method is provided in the skeletonThe neighbors method is arguably a bit tedious. If you want, you're welcome to use our solution. If you do this, make sure to cite your source (like you should every time you get significant help from anyone else online or in person).
Corner cases: You may assume that the constructor receives an N-by-N array containing the N2 integers between 0 and N2 − 1, where 0 represents the blank square. The tileAt() method should throw a java.lang.IndexOutOfBoundsException unless both i and j are between 0 and N − 1.
Performance requirements: Your implementation should support all Board methods in time proportional to N2 (or faster) in the worst case.
Goal Distance Estimates
We consider two goal distance estimates:
- Hamming estimate: The number of tiles in the wrong position.
- Manhattan estimate: The sum of the Manhattan distances (sum of the vertical and horizontal distance) from the tiles to their goal positions.
For example, the Hamming and Manhattan estimates of the board below are 5 and 10, respectively.
8 1 3 1 2 3 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
4 2 4 5 6 ---------------------- ----------------------
7 6 5 7 8 1 1 0 0 1 1 0 1 1 2 0 0 2 2 0 3
initial goal Hamming = 5 + 0 Manhattan = 10 + 0The Manhattan estimate will always be greater than or equal to the Hamming estimate. Both estimates will always be less or than equal to the true distance (try to convince yourself why).
A Deeper Look at A* (optional)
As an aside, we can make a key observation which gives insight into why A* works: To solve the puzzle from a given search node on the priority queue, the total number of moves we need to make (including those already made) is at least its priority, using either the Hamming or Manhattan estimate. (For the Hamming estimate, this is true because each tile that is out of place must move at least once to reach its goal position. For the Manhattan estimate, this is true because each tile must move its Manhattan distance from its goal position. Note that we do not count the blank square when computing the Hamming or Manhattan estimates.) Consequently, when the goal board is dequeued, we have discovered not only a sequence of moves from the initial board to the goal board, but one that makes the fewest number of moves. (Challenge for the mathematically inclined: prove this fact.)
One way to view the computation is as a game tree, where each search node is a node in the game tree and the children of a node correspond to its neighboring search nodes. The root of the game tree is the initial search node; the internal nodes have already been processed; the leaf nodes are maintained in a priority queue; at each step, the A* algorithm removes the node with the smallest priority from the priority queue and processes it (by adding its children to both the game tree and the priority queue).
Solver Test Client
We've provided two puzzle solvers that use your Solver class. These are EightPuzzleSolver.java and WordPuzzleSolver.java. Do not modify these files. 8-Puzzle input files are provided in the input folder.
The input and output format for a board is the board size N followed by the N-by-N initial board, using 0 to represent the blank square. An example of an input file for N = 3 would look something like this:
3
0 1 3
4 2 5
7 8 6Your program should work correctly for arbitrary N-by-N boards (for any 1 < N < 32768), even if it is too slow to solve some of them in a reasonable amount of time. Note N > 1.
To test against input, run the following command from the hw3 directory after compiling:
java hw3.puzzle.Solver [input file]Or in IntelliJ, set the command line arguments up using the Edit Configurations option (in the spirit of building independence see Google). As an example, if I tested against an input file input/test01.in with the following contents:
2
1 2
0 3I should get the following output:
$ java hw3.puzzle.Solver input/test01.in
Minimum number of moves = 1
2
1 2
0 3
2
1 2
3 0Optional
Try modifying the Word class so that neighbors is constant time instead of linear time. Try out the solver with a large words file, for example the one you used for project 1A. Report any cool findings on Piazza.
Optional Ultra-Edition
Try implementing other WorldState puzzles and show that your Solver is capable of solving them. Examples include maze traversal, path finding for video game AI, and solving a Rubik's Cube.
FAQ
The neighbors() method provided doesn't work. It looks like it only returns the initial board.
It works, but it does depend on the board being immutable. See the provided TestBoard.java to verify that your Board class is immutable. If you don't have this test file then use git pull skeleton master as it was added 3/19/17.
How do I know if my Solver is optimal?
The shortest solution to puzzle4x4-hard1.txt and puzzle4x4-hard2.txt are 38 and 47, respectively. The shortest solution to "puzzle*[T].txt" requires exactly T moves. Warning: puzzle36.txt, puzzle47.txt, and puzzle49.txt, and puzzle50.txt are relatively difficult.
I run out of memory when running some of the large sample puzzles. What should I do?
You should expect to run out of memory when using the Hamming priority function. Be sure not to put the JVM option in the wrong spot or it will be treated as a command-line argument, e.g.
java -Xmx1600m hw3.puzzle.Solver input/puzzle36.txtMy program is too slow to solve some of the large sample puzzles, even if given a huge amount of memory. Is this OK?
You should not expect to solve many of the larger puzzles with the Hamming priority function. However, you should be able to solve most (but not all) of the larger puzzles with the Manhattan priority function.
Even with the critical optimization, the priority queue may contain two or more search nodes corresponding to the same board. Should I try to eliminate these?
In principle, you could do so with a set data type such as java.util.TreeSet or java.util.HashSet (provided that the Board data type were either Comparable or had a hashCode() method). Try it out and see if it helps -- though make sure you don't use too much memory. If you do, the grader is likely to crash in weird ways. If you take 188, you'll learn that this version of A* is called A* Graph Search, whereas the version given in the spec is called A* Tree Search.
What size puzzles are we expected to solve?
Here are the puzzles you are explicitly expected to solve:
input/puzzle2x2-[00-06].txt
input/puzzle3x3-[00-30].txt
input/puzzle4x4-[00-30].txt
input/puzzle[00-31].txtThe puzzles work fine on my computer, but not on the AG. I'm getting a GC overhead limit exceeded error, or just a message that the "The autograder failed to execute correctly."
Your computer is probably more powerful than the autograder. Notably, the AG has much less memory. You should be able to complete puzzles 30 and 31 in less than a second, and they should also work if you use only 128 megabytes of memory. To run your code with only 128 megabytes, try running your code with the following commands. Unfortunately, there's no easy way to do this in IntelliJ. For directions in IntelliJ see this link.
java -Xmx128M hw3.puzzle.Solver ./input/puzzle30.txt
java -Xmx128M hw3.puzzle.Solver ./input/puzzle31.txt
java -Xmx128M hw3.puzzle.Solver ./input/puzzle4x4-30.txtIf your code is taking longer, by far the most likely issue is that you are not implementing the first critical optimization properly. Another possiblity is that you are creating a hash table of every board ever seen, which may cause the AG computer to run out of memory.
It is not enough to simply look at your code for the optimization and declare that it is correct. Many students have indicated confidence in their optimization implementation, only to discover a subtle bug. Use print statements or the debugger to ensure that a board never enqueues the board it came from.
Situations that cover 98% of student performance bugs:
- Recall that there is a difference between
==andequals. - Recall also that the optimization is that you should not "enqueue a neighbor if its board is the same as the board of the previous search node". Checking vs. the current board does nothing, since a board is never its own neighbor.
How do I ensure my Board class immutable?
The most common situation where a Board is not immutable is as follows:
- Step 1: Create a 2D array called cowmoo.
- Step 2: Pass cowmoo as an argument to the Board constructor.
- Step 3: Change one or more values of cowmoo.
If you just copy the reference in the Board constructor, someone can change the state of your Board by changing the array. You should instead make a copy of the 2D array that is passed to your board constructor.
Why can't Gradescope compile my files even though I can compile them locally?
Due to the nature of the autograder, you cannot use any public Board and Solver methods that were not mentioned in the spec. Consider moving the logic into one file.
The AG is reporting a bug involving access$ or some kind of null pointer exception. What's going on?
It's important that your moves and solutions methods work no matter the order in which they are called, and no matter how many times they are called. Failing the mutability test, or failing only moves but not solutions tests are sure signs of this issue.
Credits
This assignment was inspired by a somewhat similar assignment created by Kevin Wayne and Bob Sedgewick at Princeton University.